from “How To Solve It” by G. Polya, pp 1-22
The students should have some ideas of their own, some initiative. If the teacher, having watched sharply, cannot detect any signs of such initiative, he has to resume carefully his dialogue with the students. He must be prepared to meet often with the disconcerting silence of the student (which will be indicated by dots . . . . .)
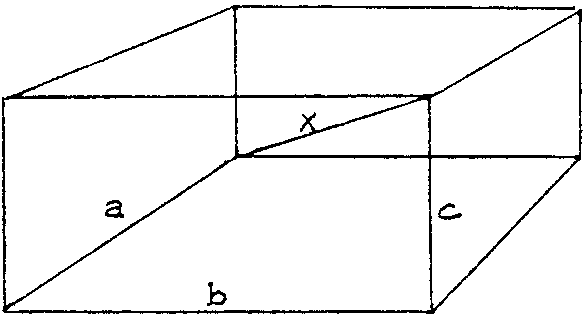
Find the diagonal of a rectangular parallelepiped of which the length, the width, and the height are known.
. . . . .
What is the unknown?
The length of the diagonal of a parallelepiped.
What are the data?
The length, the width, and the height of the parallelepiped.
Introduce suitable notation. Which letter should denote the unknown?
x.
Which letters would you choose for the length, the width, and the height?
a, b, c.
Draw a sketch to help you visualize the problem. Incorporate your notation.

Is it a reasonable problem? I mean, are the data sufficient to solve the problem?
Yes they are. If we know a, b, c, we know the parallelepiped. If the parallelepiped is determined, the diagonal x is determined.
Do you know a related problem to help you with this one?
. . . . .
Look at the unknown! Do you know a problem having the same unknown?
. . . . .
Well, what is the unknown?
The diagonal of the parallelepiped.
Do you know any problem with the same unknown?
No. We have not had any problem yet about the diagonal of a parallelepiped.
Do you know any problem with a similar unknown?
. . . . .
You see, the diagonal is a segment, the segment of a straight line. Did you never solve a problem whose unknown was the length of a line?
Of course, we have solved such a problem. For instance, to find a side of a right triangle.
Good! Here is a problem related to yours and solved before. Could you use it?
. . . . .
You were lucky enough to remember a problem which is related to your present one and which you solved before. Could you introduce some auxiliary element in order to make its use possible?
. . . .
Look here, the problem you remembered is about a triangle. Have you any triangle in your figure? .
No. Oh, but by adding a line y, like this, the unknown x becomes part of a triangle.
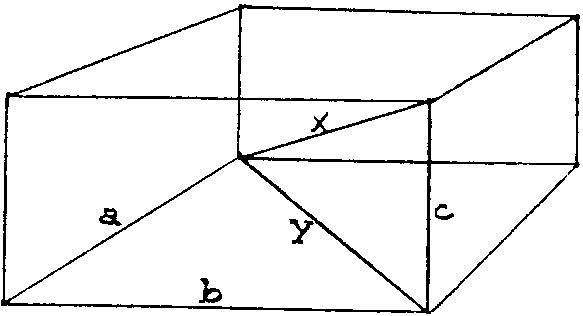
I think that was a good idea. You now have a triangle; but have you the unknown?
The unknown is the hypotenuse of the triangle; we can calculate it by the theorem of Pythagoras.
You can if both legs are known; but are they?
One leg c is given. And the other leg y is not difficult to find. Yes, y is the hypotenuse of another right triangle.
Very good! Now I see that you have a plan. Carry it out.
x2 = y2 + c2
y2 = a2 + b2
x2 = a2 + b2 + c2
x = (a2 + b2 + c2)0.5
Can you check the result? (The teacher cannot expect a good answer to this question from inexperienced students. The students, however, should acquire fairly early the experience that...if the problem is given “in letters” its result is accessible to several tests to which a problem “in numbers” is not susceptible at all. The teacher can ask several questions about the result which the students may readily answer with “Yes,” but an answer “No” would show a serious flaw in the results.)
Did you use all the data?
Is the expression you obtained for the diagonal symmetric in a, b, c? Does it remain unchanged when a, b, c are interchanged?
If the height c decreases, and finally vanishes, the parallelepiped becomes a rectangle. If you put c = 0 in your formula, do you obtain the correct formula for the diagonal of the rectangle?
If the height c increases, the diagonal increases. Does your formula show this?
The teacher’s method of questioning in the foregoing...is essentially this: Begin with a general question or suggestion, and, if necessary, come down gradually to more specific and concrete questions or suggestions till you reach one which elicits a response in the student’s mind.
The suggestions must be simple and natural because otherwise they cannot be unobtrusive.
The suggestions must be general, applicable not only to the present problem but to problems of all sorts, if they are to help develop the ability of the student and not just a special technique.
Our method admits a certain elasticity and variation, it admits various approaches, it can be and should be so applied that questions asked by the teacher could have occurred to the student himself. Suppose, for example, with the best intention to help the student, the question may be offered: Could you apply the theorem of Pythagoras? Even if he understands the suggestion the student can scarcely understand how the teacher came to the idea of putting such a question. And how could he, the student, find such a question by himself? It appears as an unnatural surprise, as a rabbit pulled out of a hat; it is really not instructive.
G. Polya